Homer Simpson vs Fermat

Vi ricordate di Homer? Personaggio principale del cartone animato “I Simpson”, grande mangiatore di ciambelle, formidabile bevitore di birra Duff e qualche volta, brillante matematico.

Tra una pausa e l’altra al bar di Boe, anche a lui piace divertirsi con formule ed equazioni matematiche. In particolare, nella puntata “La paura fa novanta VI” Homer viene catapultato in uno spazio cartesiano virtuale a tre dimensioni, ed è qui che alle sue spalle compare la formula 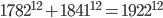 che, se fosse vera, smentirebbe l’ultimo teorema di Fermat e la dimostrazione di Andrew Wiles!

Infatti Pierre de Fermat nel 1637 affermò che non esistono soluzioni intere positive per 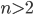della seguente equazione: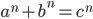

Fermat non ne diede una dimostrazione scrivendo ai margini di una copia dell’Arithmetica di Diofanto: “Dispongo di una meravigliosa dimostrazione di questo teorema, che non può essere contenuta nel margine troppo stretto della pagina”. Dopo ben sette anni di “studio matto e disperatissimo” nel 1994 Wiles ne diede la dimostrazione.

Fortunatamente il duro lavoro di Fermat e Wiles non è stato inutile, l’equazione non è corretta. Se si svolge il calcolo con una normale calcolatrice a 10 cifre il risultato è esattamente quello alle spalle di Homer, ma questo perché è l’arrotondamento a farlo apparire corretto, infatti se facessimo il calcolo con una calcolatrice di almeno 13 cifre ci accorgeremo che invece è sbagliato. Inoltre il primo membro dell’equazione è pari, il secondo dispari, di conseguenza il risultato non può essere un numero pari.Homer coglie la sfida e ci riprova! Nella puntata “L’inventore di Springfield“, fornito di occhiali e gessetto, scrive alla lavagna la seguente equazione:

Questa volta Homer sembra davvero aver smentito il teorema di Fermat. Niente paura! Se utilizziamo una buona calcolatrice scopriamo che anche questa non è un’eguaglianza esatta.

L’artefice delle due equazioni, che hanno in un primo momento impaurito i matematici, è David X Cohen, sceneggiatore e produttore televisivo, laureato in fisica all’Università di Harvard e con un master in informatica teorica a Berkeley. Cohen ha dichiarato : “Avrei preferito vivere la mia intera vita come ricercatore. Ma penso che “I Simpson” rendano divertente la matematica”. E aggiunge: “Con quest’idea in testa dormo tranquillo, e non mi rimorde la coscienza“. Insieme a lui altri studiosi di matematica e fisica sono passati dai banchi di rinomate università al gruppo di sceneggiatori del cartone animato, proprio per questo la matematica investe così spesso il mondo di Springfield. Emblematica, a tale proposito, l’affermazione riguardo “I Simpsons” di Simon Singh, scrittore britannico specializzato in divulgazione scientifica: “..un complotto pluridecennale per insegnare segretamente la matematica agli spettatori dei cartoni animati.”

Approfondimento tratto da www.wired.com

“Quello è infinito, questo è infinito. Sottraendo questo infinito a quell’infinito, ciò che resta è infinito”
Isavasya Upanishad

Fu di David Hilbert, matematico tedesco vissuto fra il IX-XX secolo, l’idea di spiegare alcune caratteristiche del concetto di infinito attraverso il paradosso del Grand Hotel, come viene fatto nel video di Open Learn qui di seguito:

Hilbert immagina un Hotel molto grande, talmente grande da avere un numero infinito di camere, ed un numero infinito di clienti che le occupano.

Una sera si presenta un viaggiatore che chiede di soggiornare al Grand Hotel. Cosa deve fare il Direttore? La soluzione è semplice, il Direttore chiede ad ogni ospite di spostarsi nella camera accanto alla propria. Ad esempio, il cliente della stanza 1 si sposterà nella 2 , quello della 2 nella 3 , e quello della stanza n nella stanza n+1.

Il giorno dopo arriva un pullman con un numero infinito di viaggiatori. Qui la situazione si complica, ma il direttore non si perde d’animo. Chiede ad ogni cliente di spostarsi nella camera con il numero doppio rispetto a quella occupata, ovvero chi occupa la stanza 1 si sposta nella , il cliente della 2 si sposta nella , quello della stanza si sposta nella . In questo modo resteranno libere le camere dispari, naturalmente infinite.

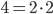
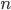
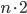
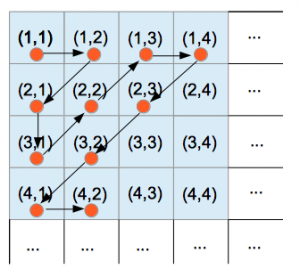Hilbert complica ancora di più la situazione immaginando che infiniti hotel con infiniti clienti falliscano. Cosa si deve fare per poter ospitare tutti gli infiniti nuovi ospiti? Il Direttore ha una brillante intuizione matematica: bisogna creare una tabella dei clienti, dove il numero di righe indica l’Hotel di provenienza e il numero di colonne la camera occupata in quell’Hotel. È importante quindi contare tutti i nuovi clienti mettendoli in fila, muovendosi su questa tabella infinita in qualche modo, così da potersi riportare nella situazione precedente: ad esempio (1,1) nella stanza 1, (1,2) nella 2, (2,1) nella 3 e così via, come mostra la figura qui a fianco.

Quello che si evince è che l’infinito ha un comportamento molto misterioso e affascinante. Nel primo esempio ci accorgiamo che aggiungere un elemento a un insieme infinito non cambia il numero di elementi dell’insieme e già questo è paradossale se vi immaginate un insieme con un numero finito di elementi.

Il secondo ci dice che anche aggiungendo un numero infinito di elementi, il numero di elementi dell’insieme rimane lo stesso infinito. Bisogna fare un’altra osservazione sul secondo esempio: ad ogni numero naturale possiamo associare uno ed un solo numero pari mediante l’operazione di raddoppio e viceversa. Questo significa che stiamo mettendo in corrispondenza biunivoca l’insieme dei numeri naturali con l’insieme dei numeri pari, e che quindi hanno lo stesso numero di elementi.

Nell’ultimo caso possiamo immaginare le coppie di numeri della tabella come numeratore e denominatore di una frazione, la scelta di metterli tutti in fila ci permette di contare tutte le frazioni e ci dice quindi che anche l’insieme dei numeri razionali ha lo stesso numero di elementi dei numeri naturali. Pensate che solo fra 0 e 1 ci sono infiniti razionali.

L’insieme dei numeri naturali è un sottoinsieme dei razionali così come l’insieme dei numeri pari è un sottoinsieme dei naturali, quindi abbiamo messo in corrispondenza biunivoca un insieme con un suo sottoinsieme proprio! “Il tutto è maggiore di una sua parte“? In questo caso forse no…

L’Hotel di Hilbert riesce a risolvere, anche se non in modo molto confortevole per gli ospiti, tutti i problemi quando si tratta di infinità numerabili di elementi (cioè che si possono mettere in fila e contare), purtroppo però non quando abbiamo a che fare con infiniti di ordine superiore (ad esempio i numeri reali).