- Il gioco della vita: ognuno ha le sue regole
- Azzardo o abilità? Percorso sul calcolo delle probabilità
- La matematica in rete
- Stiamo forse dando i numeri?
- Matematica tra le nuvole
- L’altra faccia della geometria: le Sfere di Lénárt
- Geometria e illusioni ottiche
- Pigreco!
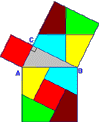
- Il teorema di Pitagora
- Geometria del foglio di carta
- I numeri di Fibonacci e il rapporto aureo
- La geometria delle carte geografiche
- La geometria della sfera
- La matematica delle bolle di sapone
- Giochi matematici
- Giochi di strategia
Il gioco della vita: ognuno ha le sue regole
Uno sguardo sul mondo della matematica dei sistemi complessi partendo da fenomeni naturali straordinariamente semplici: mettiti alla prova con i modelli matematici che simulano gli “automi cellulari”, oppure con Conway Life per vedere come da semplici regole di base si possa costruire un mondo reale estremamente complesso. Il laboratorio si propone di avvicinare i ragazzi, in modo semplice ed interattivo, al mondo della matematica, attraverso lo studio delle leggi che governano l’evoluzione di fenomeni naturali: dietro il loro aspetto elementare si cela una sorprendente varietà di comportamenti e strutture spiegabili con la matematica.
Azzardo o abilità? Percorso sul calcolo delle probabilità
Come è nato il moderno calcolo delle probabilità? Nel diciassettesimo secolo due matematici, Fermat e Pascal ne gettarono le basi dopo essersi cimentati su un problema scaturito da un gioco d’azzardo con i dadi. Quanta matematica c’è nel gioco d’azzardo? Che cos’è la rovina del giocatore? E la famosa legge dei grandi numeri? In questo percorso cercheremo di sfatare gli errori di concezioni più comuni legati al calcolo delle probabilità e vedremo come la matematica ci può aiutare a non buttare i nostri soldi. Proporremo ai ragazzi alcuni semplici giochi con i dadi e con le carte per spiegare in modo divertente i concetti basilari della probabilità, fino ad arrivare con i più grandi a trattare problemi più complicati e inerenti alla vita reale. Si parlerà inoltre di statistiche e di come spesso vengano usate in modo scorretto per fornire informazioni fallaci. A partire dalle informazioni che ci vengono direttamente dai giornali cercheremo di scoprire in
modo critico le tecniche utilizzate nelle statistiche riportate.
La matematica in rete
Dalle reti energetiche ai social network, da internet ai reticoli Steiner e alla minimizzazione dell’energia. Che cosa sono le reti e quanto sono importanti nella moderna società? Un percorso di un paio d’ore ci aiuterà a capire a cosa servono le varie tipologie di reti, conosciute e un po’ più sconosciute, e le loro potenzialità. Durante il laboratorio affronteremo esempi concreti e simulazioni al calcolatore e scopriremo la matematica che c’è dietro; le relazioni tra il gioco dei ponti di Konisberg e l’ottimizzazione dei percorsi; la matematica dietro Google e Facebook; internet e l’algoritmo della formica di Langton; la differenza tra un calcolatore e una rete neurale.
Stiamo forse dando i numeri?
Quanta superificie bisogna ricoprire con i pannelli solari per soddisfare al fabbisogno energetico dell’Italia? Quanta energia dovrei produrre, ad esempio correndo, per tenere accesa una semplice lampadina da 40 WATT per 1 minuto? Quanta energia in più dovremmo produrre all’anno se anche i cinesi avessero il nostro stesso fabbisogno energetico individuale medio? Quanti pannelli solari corrispondono ad una centrale nucleare?
Ci sono domande sull’energia a cui nessuno riesce a dare una risposta certa. Durante il laboratorio proveremo a confrontare i vari tipi di energia per vedere come funzionano dal punto di vista matematico le fonti energetiche. Ci sono domande a cui diversi esperti danno risposte diverse. Si parlerà anche di acqua e di rifiuti. L’importante non è credere all’uno o all’altro esperto ma porsi delle domande e dubitare sempre delle risposte altrui.
Matematica tra le nuvole
Si dice che il minimo battito d’ali di una farfalla sia in grado di provocare un uragano dall’altra parte del mondo. Il famoso effetto farfalla: ma di cosa si tratta? È davvero impossibile prevedere il comportamento di alcuni sistemi che sembrano imprevedibili come i modelli meteorologici? Perché caos deterministico? A questa e ad altre domande si cercherà di dare una risposta attraverso la matematica del caos. In un percorso fatto di pendoli multipli, attrattori strani, mappe del fornaio, oggetti frattali, si arriverà a definire alcuni sistemi dinamici caotici. Ci si addentrerà in modelli matematici che, seppur semplici, sono in grado di generare andamenti estremamente complessi, tanto da risultare quasi indistinguibili da processi aleatori.
Sarà dunque evidente come lo stesso fenomeno possa passare da un’evoluzione deterministica prevedibile ad una imprevedibile, a causa della sensibilità alle condizioni iniziali del regime caotico.
Per captare l’ordine e la logica nascosta di tali sistemi dinamici è necessaria una conoscenza approfondita di modelli matematici iterativi e modelli geometrici frattali. Nel laboratorio si forniranno, anche attraverso simulazioni al computer, i primi strumenti per affrontare questa nuova matematica.
L’altra faccia della geometria: le Sfere di Lénárt
Che cos’è una linea retta? Che cos’è un angolo? E un triangolo? Siete sicuri di conoscere bene le definizioni di questi oggetti? 
Le sfere di Lénárt sono strumenti didattici efficaci per capire le basi della geometria non-euclidea e “ripensare” alla definizione degli oggetti geometrici. Queste attività che chiamiamo di geometria comparativa permettono ai ragazzi esplorare un nuovo mondo e nello stesso tempo di capire meglio la geometria piana, guardandola da un punto di vista diverso. L’uso delle sfere si può adattare ad ogni livello scolastico e sono molto indicate anche per gli alunni della scuola primaria la cui familiarità con la geometria piana è ancora nella fase iniziale.
Il teorema di Pitagora
Il teorema più famoso della matematica può essere affrontato da molti punti di vista. Il laboratorio punta a farne scoprire gli aspetti geometrici, a differenza dell’approccio scolastico tradizionale che privilegia gli esercizi numerici. I ragazzi esploreranno scomposizioni, puzzles, costruzioni dinamiche, dimostrazioni di vario tipo. Vedranno anche le generalizzazioni a figure diverse dai quadrati, incontrando così, in un contesto diverso, anche l’idea di similitudine.
La geometria delle carte geografiche
L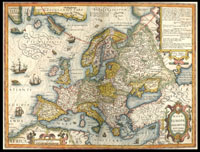
e carte geografiche non sono tutte uguali: osservandone l’evoluzione nel corso dei secoli si possono incontrare molti problemi che hanno influito profondamente sullo sviluppo della matematica. Un percorso di grande suggestione estetica, in cui la matematica si intreccia con questioni di navigazione, problemi geopolitici e commerciali.
Geometria e illusioni ottiche
I nostri occhi possono venire ingannati: le illusioni ottiche sono spesso sorprendenti. Dietro questi fenomeni ci sono anche “errori di geometria” compiuti dal nostro cervello. I ragazzi indagheranno e costruiranno alcune illusioni famose, ed altre meno note.
La geometria del foglio di carta
Un percorso di lavoro su un oggetto di uso quotidiano: il foglio A4. I ragazzi incontreranno le proporzioni, le similitudini, le radici quadrate, il calcolo approssimato, la nozione di densità… un modo per scoprire come la realtà di tutti i giorni sia intrisa di matematica.
Pigreco!
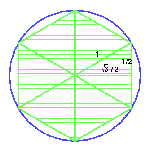Come misurare la lunghezza della circonferenza? Come calcolare l’area del cerchio? Un percorso storico-matematico, in cui i ragazzi più grandi si cimenteranno anche con un algoritmo esplicito e sorprendente per il calcolo esplicito dei decimali del numero più famoso. Un modo per iniziare a scoprire cosa sono i numeri reali.
I numeri di Fibonacci e il rapporto aureo
Tutti ne parlano, persino nei romanzi. Il laboratorio permette di scoprire, armati di calcolatrice e di altri strumenti, molte situazioni in cui compaiono questi onnipresenti numeri.
La matematica delle bolle di sapone
Da bambini sicuramente abbiamo tutti giocato a fare le bolle di sapone. Queste bolle dai mille colori iridescenti ci affascinavano, ci stupivano, forse ci facevano sognare, certamente ci intrigavano. Perché sono tutte rotonde? Perché sono trasparenti ma anche così colorate? Perché senza sapone non vengono? Diventando più grandicelli le domande si sono un po’ evolute: perché la Terra è rotonda? E le arance, le goccioline d’acqua, i pianeti? Attraverso un viaggio per tutti tra arte e scienza cercheremo di dare qualche risposta alla domanda: “Ma questa natura da che cosa è regolata?”. E ci faremo aiutare dalle bolle di sapone!
L’intento è di ritagliare degli spazi per parlare di matematica e fisica in modo non convenzionale ma corretto, per riuscire a coinvolgere tutti, grandi e piccoli in un percorso di esperimenti e attività che hanno come filo conduttore il concetto di minimizzazione dell’area.
Giochi matematici
Il laboratorio propone alcuni giochi che coinvolgono tutta la classe su questioni che riguardano diversi aspetti della matematica scolastica e non. L’uso della modalità gioco, enigma, rompicapo da una parte facilita l’osservazione del docente delle abilità e conoscenze effettivamente possedute dallo studente anche dopo qualche tempo dallo studio delle questioni trattate e dall’altra permette agli studenti di confrontarsi con una matematica meno prevedibile di quella incontrata nella pratica scolastica usuale. Alcuni dei giochi proposti sono tratti dai circuiti di giochi matematici.
Giochi di strategia
Da un grande “classico moderno” come Hex al semplicissimo ma intrigante Germogli, dal Nim all’antico gioco africano Oware, i giochi proposti permettono partite veloci, divertenti e stimolanti. L’obiettivo è sviluppare, attraverso giochi di strategia, la capacità di analizzare una situazione, rispettare le regole del gioco, elaborare tattiche efficaci, pianificare strategie, esaminare razionalmente il comportamento proprio e altrui. In dettaglio il lavoro che è possibile fare utilizzando i giochi di strategia è:
- esplicitare in una situazione le cose sottintese o evidenti
- decomporre un problema in passi semplici poi ricomporre i risultati ottenuti
- concatenare le affermazioni
- elencare e classificare i casi possibili
- dare correttamente e utilizzare definizioni
- verificare le proprie ipotesi con esempi e controesempi
- generalizzare i propri risultati
- utilizzare le ipotesi per giustificare le proprie affermazioni
