“Quello è infinito, questo è infinito. Sottraendo questo infinito a quell’infinito, ciò che resta è infinito”
Isavasya Upanishad
Fu di David Hilbert, matematico tedesco vissuto fra il IX-XX secolo, l’idea di spiegare alcune caratteristiche del concetto di infinito attraverso il paradosso del Grand Hotel, come viene fatto nel video di Open Learn qui di seguito:
Hilbert immagina un Hotel molto grande, talmente grande da avere un numero infinito di camere, ed un numero infinito di clienti che le occupano.
Una sera si presenta un viaggiatore che chiede di soggiornare al Grand Hotel. Cosa deve fare il Direttore? La soluzione è semplice, il Direttore chiede ad ogni ospite di spostarsi nella camera accanto alla propria. Ad esempio, il cliente della stanza 1 si sposterà nella 2 , quello della 2 nella 3 , e quello della stanza n nella stanza n+1.
Il giorno dopo arriva un pullman con un numero infinito di viaggiatori. Qui la situazione si complica, ma il direttore non si perde d’animo. Chiede ad ogni cliente di spostarsi nella camera con il numero doppio rispetto a quella occupata, ovvero chi occupa la stanza 1 si sposta nella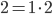 
, il cliente della 2 si sposta nella 
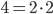, quello della stanza 
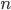si sposta nella 
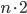. In questo modo resteranno libere le camere dispari, naturalmente infinite.
Hilbert complica ancora di più la situazione immaginando che infiniti hotel con infiniti clienti falliscano. Cosa si deve fare per poter ospitare tutti gli infiniti nuovi ospiti? Il Direttore ha una brillante intuizione matematica: bisogna creare una tabella dei client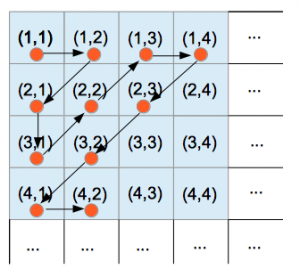
i, dove il numero di righe indica l’Hotel di provenienza e il numero di colonne la camera occupata in quell’Hotel. È importante quindi contare tutti i nuovi clienti mettendoli in fila, muovendosi su questa tabella infinita in qualche modo, così da potersi riportare nella situazione precedente: ad esempio (1,1) nella stanza 1, (1,2) nella 2, (2,1) nella 3 e così via, come mostra la figura qui a fianco.
Quello che si evince è che l’infinito ha un comportamento molto misterioso e affascinante. Nel primo esempio ci accorgiamo che aggiungere un elemento a un insieme infinito non cambia il numero di elementi dell’insieme e già questo è paradossale se vi immaginate un insieme con un numero finito di elementi.
Il secondo ci dice che anche aggiungendo un numero infinito di elementi, il numero di elementi dell’insieme rimane lo stesso infinito. Bisogna fare un’altra osservazione sul secondo esempio: ad ogni numero naturale possiamo associare uno ed un solo numero pari mediante l’operazione di raddoppio e viceversa. Questo significa che stiamo mettendo in corrispondenza biunivoca l’insieme dei numeri naturali con l’insieme dei numeri pari, e che quindi hanno lo stesso numero di elementi.
Nell’ultimo caso possiamo immaginare le coppie di numeri della tabella come numeratore e denominatore di una frazione, la scelta di metterli tutti in fila ci permette di contare tutte le frazioni e ci dice quindi che anche l’insieme dei numeri razionali ha lo stesso numero di elementi dei numeri naturali. Pensate che solo fra 0 e 1 ci sono infiniti razionali.
L’insieme dei numeri naturali è un sottoinsieme dei razionali così come l’insieme dei numeri pari è un sottoinsieme dei naturali, quindi abbiamo messo in corrispondenza biunivoca un insieme con un suo sottoinsieme proprio! “Il tutto è maggiore di una sua parte“? In questo caso forse no…
L’Hotel di Hilbert riesce a risolvere, anche se non in modo molto confortevole per gli ospiti, tutti i problemi quando si tratta di infinità numerabili di elementi (cioè che si possono mettere in fila e contare), purtroppo però non quando abbiamo a che fare con infiniti di ordine superiore (ad esempio i numeri reali).
