I numeri primi sono numeri divisibili solamente per uno e per sé stessi, sono uno dei concetti basilari della teoria dei numeri, infatti qualsiasi numero naturale diverso da uno può essere scomposto in fattori primi, inoltre, tale scomposizione è unica. I numeri primi sono infiniti ed il più piccolo è il numero 2, tutti gli altri sono dispari in quanto ogni numero pari è divisibile per 2.
Nonostante vengano studiati sin dall’antichità (“Elementi di Euclide” 300 a.C) numerose congetture non sono ancora state dimostrate, come ad esempio l’ipotesi di Riemann e la congettura dei primi gemelli.
“I numeri primi sono ciò che rimane una volta eliminati tutti gli schemi: penso che i numeri primi siano come la vita. Sono molto logici ma non si riesce mai a scoprirne le regole, anche se si passa tutto il tempo a pensarci su”
Mark Haddon
Dalle prime congetture nel 300 a.C facciamo un salto nel 2004, anno in cui Ben Green e Terence Tao,
operando un’estensione di quello che è il teorema di Szemerédi, dimostrano uno splendido teorema sui numeri primi, affermando che la sequenza dei numeri primi contiene progressioni aritmetiche arbitrariamente lunghe e che, dato un qualsiasi numero naturale N, c’è sempre un primo 
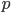e un intero positivo 
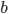, in modo che anche
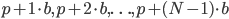
siano primi. Ad esempio, se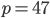 
, 
, 
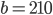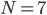avremo la seguente progressione aritmetica:
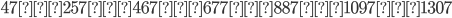
Va comunque notato che questo teorema, di difficile dimostrazione teorica, dimostra l’esistenza di queste progressioni ma non fornisce un modo per trovarle e quindi è di difficile applicazione pratica.
Terence Tao ha esteso poi i risultati alle progressioni polinomiali dimostrando che: dati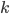 
polinomi in un’incognita 
: 
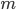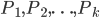con 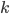intero positivo, esistono infiniti interi 
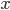e 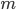tali che
