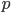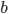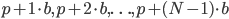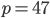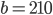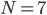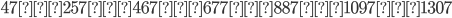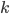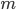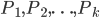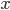Il 30 maggio 2014 si festeggiano i 200 anni dalla nascita di Eugène Charles Catalan, matematico belga, insegnante e appassionato di teoria dei numeri e teoria combinatoria. Nel 1825 iniziò i suoi studi all’École Polytechnique, famosa università parigina in cui fu anche docente di geometria descrittiva nel 1838, prima di essere frenato dalla sua attività politica: Catalan aveva infatti idee fortemente di sinistra, era un attivista politico, partecipò alle rivoluzioni del 1848 e si rifiutò di prestare giuramento all’impero.
La sua fama si deve principalmente alla famosa congettura formulata nel 1844, in una lettera all’editore del journal de Crelle:« Vi prego, signore, di voler enunciare, nella vostra raccolta, il seguente teorema, che credo vero, nonostante non sia ancora riuscito a dimostrarlo completamente: altri potranno forse essere più fortunati: Due numeri interi consecutivi diversi da 8 e 9 non possono essere entrambi potenze esatte; in altre parole, l’equazione 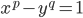a valore nei numer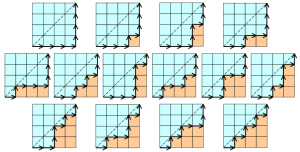i interi positivi, ammette una sola soluzione. », diventata teorema nel 2002 grazie alla dimostrazione di Preda Mihăilescu, un matematico rumeno. La dimostrazione fu verificata da Yuri Bilu e fu pubblicata nel 2004 nel Journal für die reine und angewandte Mathematik. Essa fa un largo uso della teoria dei campi ciclotomici e dei moduli di Galois.
Catalan fu poi nominato nel 1883 per essere uno dei tre giurati incaricati di stabilire un premio per una dimostrazione dell’ultimo teorema di Fermat, dall’Accademia delle Scienze belga, che ancora oggi rilascia ogni 5 anni il premio Eugène-Catalan alla personalità belga o francese che abbia illuminato con la propria ricerca aspetti ignoti di matematica pura.
Il nome di questo matematico belga viene dato anche a dei particolari numeri, scoperti intorno al 1838 da Catalan stesso nella risoluzione di un problema geometrico, ovvero: in quanti modi diversi si può suddividere un poligono convesso con 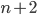lati in n triangoli, tracciandone le diagonali in modo che non si intersechino?

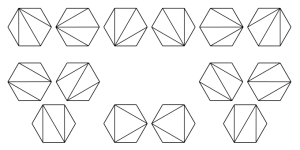
La successione di questi numeri era stata già indicata dal matematico tedesco-ungherese Jan Andrej Segner e ancora prima da Eulero, ed è una successione individuata mediante una relazione ricorsiva non lineare i cui primi termini sono:

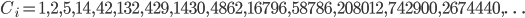
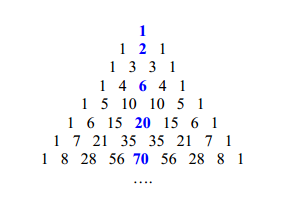
Tali coefficienti possono essere collegati al triangolo di Pascal: se li moltiplichiamo rispettivamente per 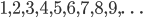otteniamo la colonna centrale del triangolo.
I numeri di Catalan sono quindi la risposta di molti problemi in matematica discreta e non una mera speculazione teorica. Si possono infatti trovare ulteriori e sorprendenti applicazioni dei numeri catalani in contesti apparentemente scorrelati.
Ad esempio è il numero delle possibili scomposizioni di un poligono regolare di lati in triangoli, tramite diagonali che però non si intersecano. Oppure è il numero possibili percorsi più brevi su una griglia quadrettata di lato , al variare del numero di quadretti , per andare da un estremo all’altro della diagonale principale senza attraversarla. O ancora il numero di coppie di parentesi possibili da collocare in un insieme di numeri che devono essere moltiplicati fra loro, due per volta.

Altre curiosità sui numeri di Catalan:
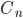–  è dispari se e solo se  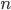  è una potenza di 2 meno 1
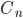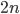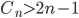– Tutti i divisori primi di  sono minori di , ma per 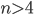, quindi  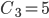è l’unico numero di Catalan primo.

Fonti:

http://webmath2.unito.it/paginepersonali/romagnoli/catalan.pdf
http://webmath2.unito.it/paginepersonali/romagnoli/ghigo.pdf
http://areeweb.polito.it/didattica/polymath/htmlS/info/Numeri/Mag10/NumeriCatlan.htm
http://it.wikipedia.org/wiki/Eug%C3%A8ne_Charles_Catalan
http://www.aromatic.org/rudi/024.pdf

I numeri primi sono numeri divisibili solamente per uno e per sé stessi, sono uno dei concetti basilari della teoria dei numeri, infatti qualsiasi numero naturale diverso da uno può essere scomposto in fattori primi, inoltre, tale scomposizione è unica. I numeri primi sono infiniti ed il più piccolo è il numero 2, tutti gli altri sono dispari in quanto ogni numero pari è divisibile per 2.

Nonostante vengano studiati sin dall’antichità (“Elementi di Euclide” 300 a.C) numerose congetture non sono ancora state dimostrate, come ad esempio l’ipotesi di Riemann e la congettura dei primi gemelli.

“I numeri primi sono ciò che rimane una volta eliminati tutti gli schemi: penso che i numeri primi siano come la vita. Sono molto logici ma non si riesce mai a scoprirne le regole, anche se si passa tutto il tempo a pensarci su”

Mark Haddon

Dalle prime congetture nel 300 a.C facciamo un salto nel 2004, anno in cui Ben Green e Terence Tao, operando un’estensione di quello che è il teorema di Szemerédi, dimostrano uno splendido teorema sui numeri primi, affermando che la sequenza dei numeri primi contiene progressioni aritmetiche arbitrariamente lunghe e che, dato un qualsiasi numero naturale N, c’è sempre un primo e un intero positivo , in modo che anche

siano primi. Ad esempio, se , , avremo la seguente progressione aritmetica:

Va comunque notato che questo teorema, di difficile dimostrazione teorica, dimostra l’esistenza di queste progressioni ma non fornisce un modo per trovarle e quindi è di difficile applicazione pratica.

Terence Tao ha esteso poi i risultati alle progressioni polinomiali dimostrando che: dati polinomi in un’incognita : con intero positivo, esistono infiniti interi e tali che

siano contemporaneamente primi.

Ulteriori approfondimenti qui